Home
Plates Strings
ICSV_2019 DAFx_2021 JASA_2021 JSV_2022 ENOC_2022
Publications About
M. Ducceschi, S. Bilbao, S. Willemsen and S. Serafin

Linearly-implicit schemes for collisions in musical acoustics based on energy quadratisation

The Journal of the Acoustical Society of America, 2021

Collisions have an important role in musical acoustics. In many musical instruments, the mechanisms responsible for sound production involve a kind of collision: examples include the hammer-string, stick-membrane and backboard-string interactions, as well as reed-beating effects in wind instruments. Collisions are strongly nonlinear, and cannot be approximated by linearisation. From a numerical standpoint, a form of control over the stability of the simulated solution is necessary. This is usually accomplised via energy methods. The work by Chatziioannou and van Walstijn [1] considered a discretisation of Hamilton's equations in first-order form, via a discrete gradient preserving a numerical Hamiltonian. Following that, Bilbao et al. [2] developed a conservative scheme in second-order form, and applied it to a large class of musical systems.

All such methods are fully-implicit, and the the update of the state variable is performed via iterative procedures such as e.g. Newton-Raphson. This results in well-known issues, including a varible operational cost, the problem of existence and uniqueness of the numerical solution, the problem of tolerance thresholds, etc.

Here, a method is proposed, such that collisions may be resolved in a single iteration, whilts guaranteeing passivity via energy conservation. This is achieved via the introduction of an auxiliary state variable, that needs to be solved for at each update along with the usual state variable such as e.g. displacement. The extra state variable has the units of square root of energy, and is always well-defined for commonly encountered non-negative potentials.

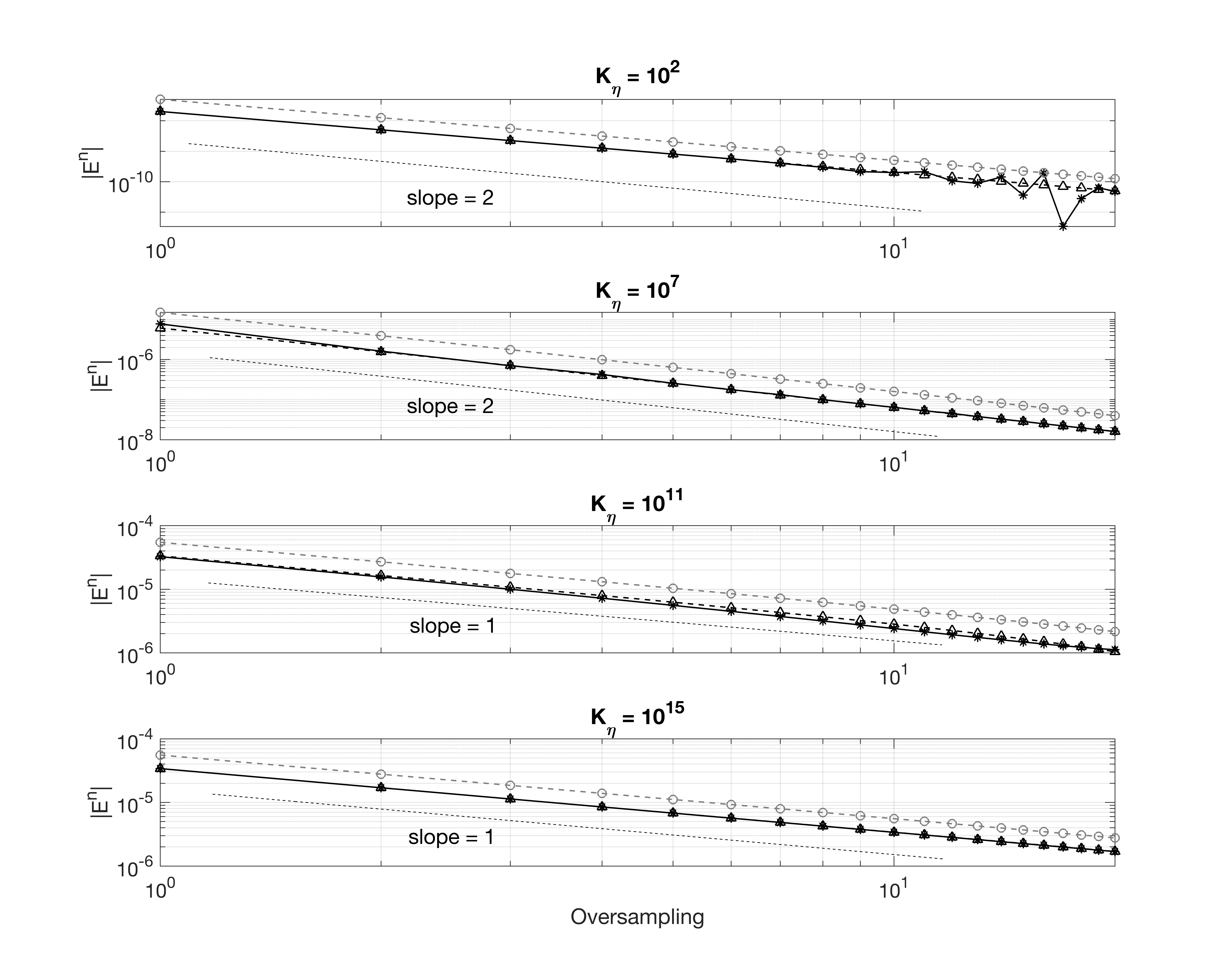
Mass-Barrier
Matlab sample code for the mass-barrier collision, comparing the non-iterative schemes to iterative methods published previously, is available here.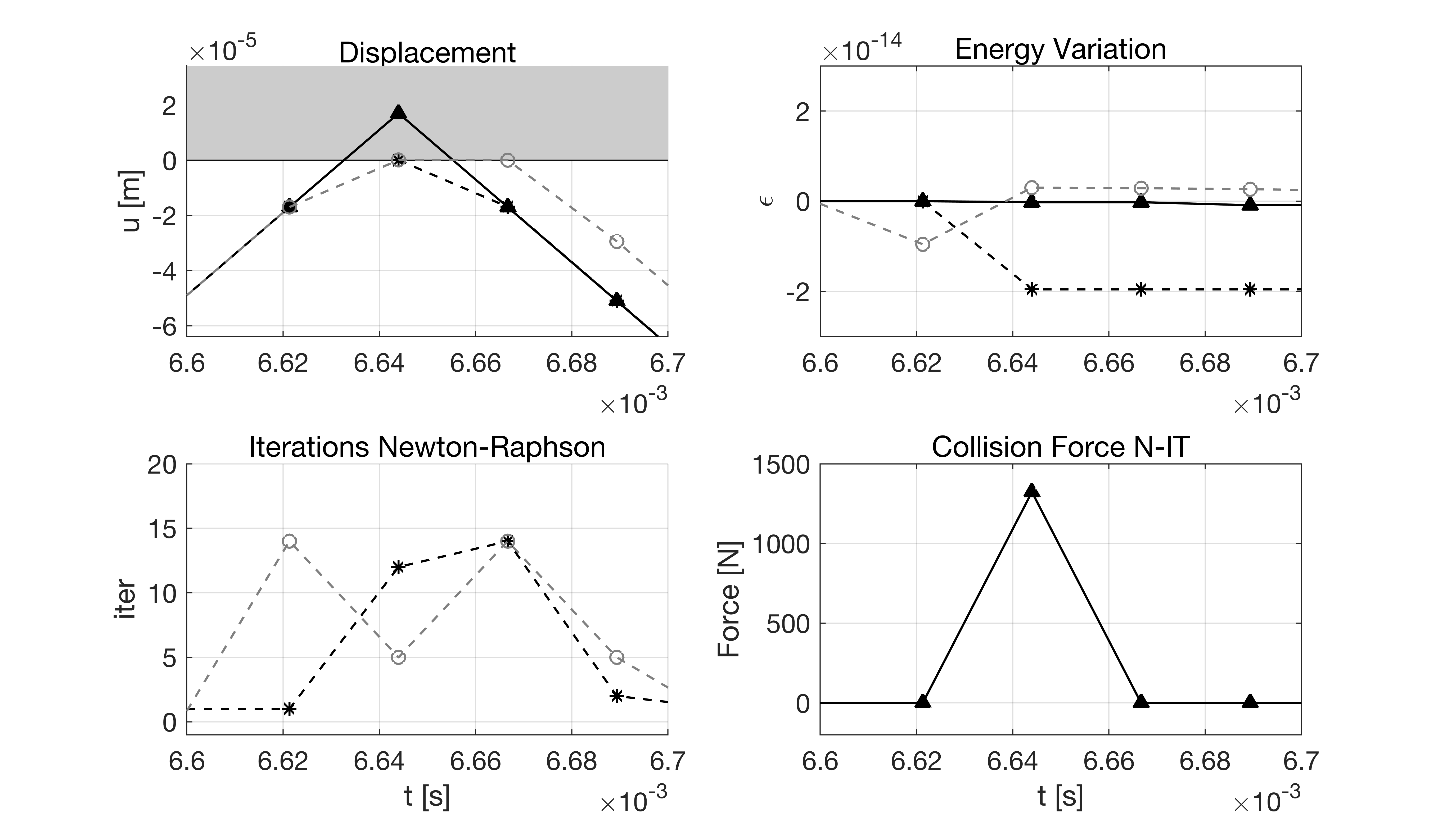

Mass-Barrier
Mass-barrier collision. In the figures, the solid line is the proposed non-iterative scheme N-IT; the blacked dashed line is as per [1], and the grey dashed line is as per [2]. Note that, for large barrier stiffness values, as in this example, a large number of Newton-Raphson iterations may be necessary. The non-iterative scheme conserves energy to machine accuracy in a single iteration.
Convergence Mass-Barrier
Convergence rates of the numerical schemes, obtained by comparing against the analytic solution available for the case of the free particle colliding against a barrier with linear restoring force. Note that, when the stiffness of the barrier becomes large, the methods become first-order accurate, as one may show by Taylor expansion arguments.

Hammer-String
As a first musical application, consider the hammer-string collision. This kind of collision takes place in stringed instruments such as the piano and the dulcimer. In the video below, the non-iterative scheme is compared to the iterative scheme presented in [2]. Matlab sample code is available here.

Hammer-string collision. The non-iterative scheme and the scheme in [2] are compared. The former is shifted up by 1mm for clarity.

Distributed Collisions
The non-iterative schemes can be extended to include collisions between fully distributed objects. Both finite difference and modal methods can be used, and the solution is computed in a single iteration per time step. Matlab sample code for the case of the string-fretboard is available here.

String-fretboard collision. The non-iterative scheme is run using a full finite difference discretisation (dashed line) and a modal discretisation (solid).

Snare-membrane collision in the snare drum. The non-iterative scheme is run using a full finite difference discretisation. The system is energy-conserving to machine accuracy, using one single iteration per time step, in spite of a large number of collisions taking place between two fully deformable distributed objects.

Snare-membrane collision. View from above highlighting wave propagation.

References
  1. V. Chatziioannou and M. van Walstijn. Energy conserving schemes for the simulation of musical instrument contact dynamics, Journal of Sound and Vibration, Vol. 339:262-279, 2015
  2. S. Bilbao, A. Torin, V. Chatziioannou. Numerical modeling of collisions in musical instruments, Acta Acustica United With Acustica, Vol. 101(1):155-173, 2015